Show That Beta Distribution Belongs to Exponential Family

Theexponential distribution is frequently concerned with the amount of time until some specific upshot occurs. For example, the amount of time (beginning at present) until an earthquake occurs has an exponential distribution. Other examples include the length, in minutes, of long altitude business telephone calls, and the amount of time, in months, a car battery lasts. It tin can exist shown, likewise, that the value of the change that y'all have in your pocket or purse approximately follows an exponential distribution.

Values for an exponential random variable occur in the following mode. In that location are fewer large values and more pocket-sized values. For instance, the corporeality of money customers spend in one trip to the supermarket follows an exponential distribution. There are more people who spend small amounts of money and fewer people who spend big amounts of money.

The exponential distribution is widely used in the field of reliability. Reliability deals with the corporeality of time a product lasts.

Example

LetX = amount of time (in minutes) a postal clerk spends with his or her client. The time is known to have an exponential distribution with the average corporeality of time equal to four minutes.

X is a continuous random variable since fourth dimension is measured. It is given that μ = four minutes. To exercise whatsoever calculations, you must know m, the decay parameter.

[latex]{m}=\frac{ane}{\mu}[/latex]. Therefore, [latex]{g}=\frac{ane}{4}={0.25}[/latex]

The standard difference, σ, is the same equally the mean. μ = σ

The distribution notation is X ~ Exp(m). Therefore, X ~ Exp(0.25).

The probability density function is f(x) = me ^–mx . The number e = 2.71828182846… It is a number that is used often in mathematics. Scientific calculators have the cardinal "due east^x ." If you enter one for x, the reckoner will display the value east.

The curve is:

f(x) = 0.25east ^–0.2510 where x is at to the lowest degree zero and m = 0.25.

For case, f(5) = 0.25e ^−(0.25)(5) = 0.072. The postal clerk spends 5 minutes with the customers. The graph is as follows:

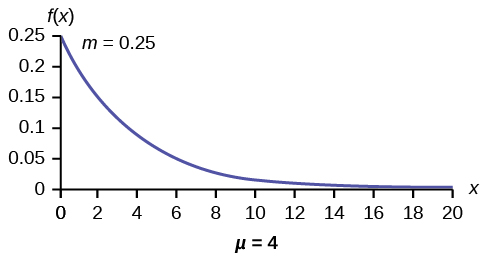
Observe the graph is a declining curve. When ten = 0,

f(x) = 0.25due east ^(−0.25)(0) = (0.25)(1) = 0.25 = m. The maximum value on the y-axis is m.

Try It

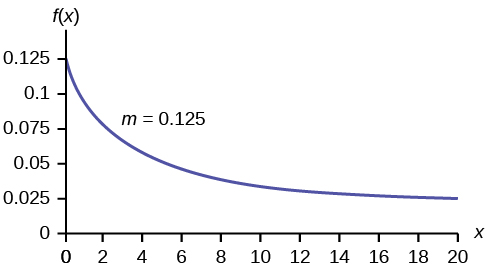
The corporeality of time spouses shop for anniversary cards can be modeled by an exponential distribution with the average amount of fourth dimension equal to 8 minutes. Write the distribution, state the probability density function, and graph the distribution.

Solution:

X ~ Exp(0.125); f(x) = 0.125e^–0.125x ;

 Example

Using the information in example 1, find the probability that a clerk spends four to five minutes with a randomly selected customer.

The bend is:

Ten ~ Exp(0.125); f(10) = 0.125e^–0.125ten

a) Find P(4 < x < five).

Solution:

The cumulative distribution function (CDF) gives the area to the left.

P(x < x) = 1 – e^–mx

P(x < 5) = ane – eastward(–0.25)(5) = 0.7135 and P(x < 4) = i – e ^(–0.25)(4) = 0.6321

Y'all can exercise these calculations easily on a computer.

 The probability that a postal clerk spends four to v minutes with a randomly selected customer is P(4 < 10 < 5) = P(ten < 5) – P(x < 4) = 0.7135 − 0.6321 = 0.0814.

On the dwelling house screen, enter (1 – e^(–0.25*5))–(1–e^(–0.25*iv)) or enter e^(–0.25*four) – eastward^(–0.25*5).

b) Half of all customers are finished inside how long? (Find the 50^th percentile)

Solution:

Find the 50^th percentile.

P(x < one thousand) = 0.50, k = 2.8 minutes (reckoner or reckoner)

Half of all customers are finished within ii.8 minutes.

You can also practice the adding every bit follows:

P(x < k) = 0.fifty and P(x < yard) = ane –eastward ^–0.25k

Therefore, 0.fifty = 1 − due east ^−0.25k and e ^−0.25m = 1 − 0.50 = 0.5

Have natural logs: ln(e ^–0.25k ) = ln(0.l). So, –0.25one thousand = ln(0.50)

Solve for k:  [latex]{k}=\frac{ln0.50}{-0.25}={0.25}=2.8[/latex] minutes

c) Which is larger, the hateful or the median?

Solution:

From part b, the median or 50^th percentile is ii.8 minutes. The theoretical mean is four minutes. The mean is larger.

 Example

The number of days ahead travelers buy their airline tickets can be modeled by an exponential distribution with the average corporeality of time equal to xv days. Find the probability that a traveler will purchase a ticket fewer than x days in advance. How many days do half of all travelers wait?

Solution:

P(x < 10) = 0.4866

50^th percentile = 10.40

Example

On the average, a certain figurer part lasts ten years. The length of time the estimator part lasts is exponentially distributed.

 a) What is the probability that a reckoner function lasts more seven years?

Solution:Let ten = the amount of time (in years) a calculator office lasts.

[latex]\mu = {10}[/latex] so m = [latex]\frac{1}{\mu} = \frac{1}{10}={0.ten}[/latex]
P(x > 7). Describe the graph.

P(x > seven) = one – P(ten < 7).

Since P(Ten < 10) = 1 –e^–mx and then P(X > 10) = one –(1 –east^–mx ) = due east^-mx

P(x > 7) = due east ^(–0.1)(7) = 0.4966. The probability that a computer part lasts more than seven years is 0.4966.

On the home screen, enter e^(-.one*7).

b) On the boilerplate, how long would five computer parts last if they are used one after another?

Solution:

On the average, one estimator office lasts 10 years. Therefore, five computer parts, if they are used one right after the other would last, on the average, (5)(x) = l years.

c) Lxxx percent of calculator parts last at virtually how long?

Solution:

Find the 80^th percentile. Draw the graph. Let k = the eighty^th percentile.

Solve for k: [latex]{1000}=\frac{ln(1-0.lxxx)}{-0.one}={16.ane}[/latex]

Eighty percent of the computer parts concluding at most 16.1 years.

Solution:

Detect P(9 < x < xi). Draw the graph.

d) What is the probability that a computer part lasts betwixt nine and 11 years?

Solution:

P(9 < ten < 11) = P(ten < 11) – P(x < 9) = (1 – e ^{(–0.1)(eleven)}) – (1 – e ^{(–0.ane)(9)}) = 0.6671 – 0.5934 = 0.0737. The probability that a computer office lasts between nine and 11 years is 0.0737.

Example

Suppose that the length of a phone call, in minutes, is an exponential random variable with decay parameter = ane 12 . If some other person arrives at a public telephone just before you, find the probability that you will have to wait more than five minutes. Permit X = the length of a phone phone call, in minutes.

What is m, μ, and σ? The probability that y'all must wait more than five minutes is _______ .

Solution:

chiliad =  [latex]\frac{i}{12}[/latex]

[latex]\mu [/latex] = 12

[latex]\sigma [/latex] = 12

P(x > 5) = 0.6592

Instance

The fourth dimension spent waiting between events is often modeled using the exponential distribution. For example, suppose that an average of 30 customers per hour arrive at a store and the time between arrivals is exponentially distributed.

1. On average, how many minutes elapse between 2 successive arrivals?
2. When the store starting time opens, how long on average does it take for iii customers to arrive?
3. After a client arrives, observe the probability that it takes less than 1 minute for the next customer to arrive.
4. Subsequently a customer arrives, observe the probability that it takes more than five minutes for the next client to arrive.
5. 70 percent of the customers arrive within how many minutes of the previous customer?
6. Is an exponential distribution reasonable for this situation?

Solutions:

1. Since we expect xxx customers to arrive per 60 minutes (60 minutes), we wait on boilerplate one customer to arrive every 2 minutes on boilerplate.
2. Since i customer arrives every 2 minutes on average, information technology will take six minutes on average for three customers to arrive.
3. Allow 10 = the time betwixt arrivals, in minutes. By office a, μ = 2, so m = 1 2 = 0.5.
   Therefore, Ten ∼ Exp(0.5).The cumulative distribution function is P(X < x) = ane – e(–0.5x) ^e .Therefore P(Ten < 1) = 1 – due east^(–0.5)(1) ≈ 0.3935

4. 

5. P(X > 5) = 1 – P(X < five) = 1 – (i – e ^(–5)(0.v)) = e^–2.v ≈ 0.0821.

6. 
7. We desire to solve 0.seventy = P(Ten < x) for x.
   Substituting in the cumulative distribution part gives 0.seventy = one – e ^–0.five10 , so that eastward ^–0.5x = 0.30. Converting this to logarithmic class gives –0.v10 = ln(0.30), or x = l n ( 0.30 ) – 0.5 ≈ 2.41 minutes.Thus, seventy percent of customers arrive within two.41 minutes of the previous customer.
8. This model assumes that a unmarried customer arrives at a fourth dimension, which may not be reasonable since people might shop in groups, leading to several customers arriving at the same time. It also assumes that the flow of customers does not change throughout the day, which is not valid if some times of the twenty-four hour period are busier than others.

Memorylessness of the Exponential Distribution

In instance 1, recall that the amount of time betwixt customers is exponentially distributed with a mean of 2 minutes (X ~ Exp (0.5)). Suppose that five minutes take elapsed since the last customer arrived. Since an unusually long amount of time has at present elapsed, it would seem to exist more likely for a customer to make it within the adjacent minute. With the exponential distribution, this is not the example–the additional time spent waiting for the adjacent customer does not depend on how much time has already elapsed since the last customer. This is referred to as the memoryless holding. Specifically, the memoryless holding says that

P (X > r + t | X > r) = P (X > t) for all r ≥ 0 and t ≥ 0

For example, if five minutes has elapsed since the terminal client arrived, and then the probability that more one minute will expire before the adjacent customer arrives is computed by using r = 5 and t = 1 in the foregoing equation.

P(10 > five + 1 | Ten > 5) = P(X > 1) = e ( – 0.5 ) ( i ) ≈ 0.6065.

This is the same probability equally that of waiting more than one minute for a client to arrive after the previous arrival.

The exponential distribution is often used to model the longevity of an electrical or mechanical device. In example ane, the lifetime of a sure calculator office has the exponential distribution with a mean of x years (X ~ Exp(0.1)). The memoryless belongings says that noesis of what has occurred in the past has no outcome on future probabilities. In this instance it means that an old part is non whatever more likely to break downwardly at any particular time than a make new part. In other words, the part stays every bit good as new until it suddenly breaks. For example, if the part has already lasted ten years, then the probability that it lasts some other seven years is P(X > 17|X > 10) =P(X > 7) = 0.4966.

Case

Refer to example 1, where the fourth dimension a postal clerk spends with his or her customer has an exponential distribution with a mean of iv minutes. Suppose a customer has spent four minutes with a postal clerk. What is the probability that he or she will spend at to the lowest degree an boosted three minutes with the postal clerk?

The decay parameter of 10 is m = 14 = 0.25, then X ∼ Exp(0.25).
The cumulative distribution part is P(Ten < x) = 1 – e–0.25x. Nosotros want to detect P(Ten > vii|X > 4). The memoryless property says that P(Ten > seven|X > 4) = P (X > 3), and so we simply need to detect the probability that a client spends more than than three minutes with a postal clerk.
This is P(Ten > iii) = 1 – P (Ten < 3) = 1 – (ane – due east–0.25⋅3) = eastward–0.75 ≈ 0.4724.

Relationship between the Poisson and the Exponential Distribution

There is an interesting relationship between the exponential distribution and the Poisson distribution. Suppose that the fourth dimension that elapses between 2 successive events follows the exponential distribution with a hateful of μ units of time. Also assume that these times are independent, pregnant that the time betwixt events is not affected by the times between previous events. If these assumptions concur, then the number of events per unit time follows a Poisson distribution with mean λ = 1/μ. Call up that if X has the Poisson distribution with hateful λ, then [latex]P(10=k)=\frac{{\lambda}^{k}{e}^{-\lambda}}{thou!}[/latex]. Conversely, if the number of events per unit of measurement time follows a Poisson distribution, then the amount of time between events follows the exponential distribution. (k! = g*(k-1*)(k–2)*(k-three)…three*2*1)

Case

At a law station in a large city, calls come in at an average rate of 4 calls per minute. Assume that the time that elapses from 1 phone call to the next has the exponential distribution. Have notation that we are concerned just with the rate at which calls come in, and nosotros are ignoring the time spent on the phone. We must likewise assume that the times spent between calls are independent. This ways that a peculiarly long delay between two calls does not mean that at that place will be a shorter waiting period for the side by side call. We may then deduce that the total number of calls received during a time menstruation has the Poisson distribution.

1. Detect the average time between two successive calls.
2. Find the probability that after a call is received, the adjacent telephone call occurs in less than 10 seconds.
3. Find the probability that exactly five calls occur within a infinitesimal.
4. Find the probability that less than five calls occur within a minute.
5. Observe the probability that more than forty calls occur in an eight-minute menses.

Solutions:

1. On boilerplate there are iv calls occur per minute, then 15 seconds, or [latex]\frac{15}{threescore} [/latex]= 0.25 minutes occur betwixt successive calls on boilerplate.
2. Permit T = fourth dimension elapsed between calls. From part a, [latex]\mu = {0.25} [/latex], and so m = [latex]\frac{1}{0.25} [/latex] = iv. Thus, T ~ Exp(4).  The cumulative distribution function is P(T < t) = ane – eastward ^–4t . The probability that the next call occurs in less than x seconds (ten seconds = 1/6 minute) is P(T < [latex]\frac{ane}{half-dozen}[/latex]) = ane –  [latex]{e}^{-4\frac{one}{half dozen}} \approx{0.4866} [/latex]
3. Permit Ten = the number of calls per minute. Every bit previously stated, the number of calls per minute has a Poisson distribution, with a mean of four calls per minute. Therefore, X ∼ Poisson(4), and so P(X = 5) = [latex]\frac{{four}^{5}{e}^{-4}}{5!}\approx[/latex] 0.1563. (5! = (5)(iv)(3)(ii)(1))
4. Go on in mind that 10 must be a whole number, and then P(Ten < 5) = P(X ≤ 4).

   To compute this, nosotros could take P(10 = 0) + P(X = 1) + P(10 = 2) + P(X = 3) + P(X = 4).

   Using engineering science, nosotros encounter that P(X ≤ 4) = 0.6288.

5. Let Y = the number of calls that occur during an eight infinitesimal period.

   Since there is an average of four calls per minute, there is an average of (8)(4) = 32 calls during each eight minute menses.

   Hence, Y ∼ Poisson(32). Therefore, P(Y > 40) = i – P (Y ≤ twoscore) = 1 – 0.9294 = 0.0707.

Concept Review

If X has an exponential distribution with mean [latex]\mu[/latex] then the decay parameter is [latex]m =\frac{ane}{\mu}[/latex], and we write Ten ∼ Exp(m) where x ≥ 0 and m > 0 . The probability density function of X is f(10) =me^-mx (or equivalently [latex]f(x)=\frac{1}{\mu}{e}^{\frac{-x}{\mu}}[/latex].The cumulative distribution function of 10 is P(X≤ ten) = 1 – e ^–mx .

The exponential distribution has the memoryless property, which says that future probabilities do not depend on any by data. Mathematically, it says that P(X > x + thou|10 > x) = P(X > 1000).

If T represents the waiting time between events, and if T ∼ Exp(λ), then the number of events X per unit time follows the Poisson distribution with mean λ. The probability density part of [latex]P\left(X=k\right)=\frac{\lambda^{k}}{e^{-\lambda}}k![/latex]. This may be computed using a TI-83, 83+, 84, 84+ calculator with the command poissonpdf(λ, k). The cumulative distribution function P(X ≤ 1000) may be computed using the TI-83, 83+,84, 84+ calculator with the command poissoncdf(λ, k).

Formula Review

Exponential: X ~ Exp(chiliad) where grand = the decay parameter

• pdf: f(x) = m[latex]{e}^{-mx}[/latex] where 10 ≥ 0 and one thousand > 0
• cdf: P(X ≤ 10) = 1 –[latex]{east}^{-mx}[/latex]
• mean [latex]\mu = \frac{1}{k}[/latex]
• standard deviation σ = µ
• percentile, k: k = [latex]\frac{ln(\text{AreaToTheLeftOfK})}{-g}[/latex]
• Additionally
  • P(X > x) = e ^(–mx)
  • P(a < 10 < b) = east ^(–ma) – e ^(–mb)
• Memoryless Property: P(X > x + k|X > x) = P (10 > yard)
• Poisson probability:P ( X = k ) =[latex]\frac{{\lambda}^{k}{eastward}^{-\lambda}}{k!}[/latex] with mean [latex]\lambda[/latex]
• g! = k*(one thousand-ane)*(k-2)*(chiliad-iii)…3*two*1

References

Data from the The states Demography Bureau.

Data from Globe Earthquakes, 2013. Available online at http://www.world-earthquakes.com/ (accessed June 11, 2013).

"No-hitter." Baseball game-Reference.com, 2013. Available online at http://www.baseball-reference.com/bullpen/No-hitter (accessed June 11, 2013).

Zhou, Rick. "Exponential Distribution lecture slides." Available online at www.public.iastate.edu/~riczw/stat330s11/lecture/lec13.pdf‎ (accessed June 11, 2013).

aguiarthandrell.blogspot.com

Source: https://courses.lumenlearning.com/introstats1/chapter/the-exponential-distribution/

Share this post